BitVM is a “Computing paradigm to express Turing-complete Bitcoin contracts”proposed by Robin Linus, which does not require a soft fork.
Bitcoin script is designed to be Turing-incomplete, making it impossible to implement arbitrary contracts like those implemented on VM-based chains. Previous proposals to realize Turing-complete contracts on Bitcoin required a soft fork to activate new opcodes. BitVM is different from these proposals as it does not require one.
Please note that it still has important limitations:
・Contracts are limited to those between two parties
・A significant amount of computation and interaction between the two parties is required (i.e., Hundreds of MB to several GB data interaction; local storage)
Despite these constraints, the proposal has spurred vibrant community debate.
The section below details how to establish contracts between a Prover, who asserts they know the answer of a specified problem, and a Verifier, who assesses the truth of that assertion.
As long as both parties are cooperative, they can jointly settle any contract.
If the Verifier does not agree that the Prover’s assertion is correct, a “Challenge and Response” scheme is initiated — this will be explained in detail later — and if the assertion’s inconsistencies are identified, the Verifier is entitled to seize the funds of the Prover.
Before touching on how BitVM works, we will provide some preliminaries.
Preliminaries
⚫️Logic Circuits
Code written in a programming language is converted into binary code (a series of 0s and 1s) by a compiler. The processor reads this binary code and executes instructions using logic circuits.
Typical examples of components that make up logic circuits include AND gates, OR gates, NOT gates, and NAND gates. NAND gates are called “universal gates” because they can be used to build up all other gates.
In the paper NAND gates are used only for the sake of the argument, to abstract away all the complexity of crafting efficient bitcoin scripts. We refer to this circuit as a “Binary Circuit”.
The author believes that
In practice using all the available bitcoin script opcodes makes onchain TXs 10x — 100x smaller than when using only NANDs.
The following figure shows a Binary Circuit with A, B, C, and D as inputs. The Prover claims that (s)he knows all inputs.
⚫️OP_NAND
Bitcoin’s existing Opcodes, OP_BOOLAND and OP_NOT can be combined to perform the functions of a NAND operation.
We refer to this combination of OP_BOOLAND and OP_NOT as “OP_NAND”.
⚫️Bit Value Commitment
The following is a script for the prover to commit to the input and output values (0 or 1) of each NAND gate: If the prover provides a preimage of hash1, `1` is pushed onto the stack. If the prover provides a preimage of hash0, `0`’ is pushed onto the stack.
We refer to these Opcode sets as “OP_BIT_COMMITMENT”.
The following is a script for the Prover to commit to a LogicGate (NAND1) by combining OP_NAND and OP_BITCOMMITMENT. When they provide the following three values, three sets of values (0 or 1), namely A, B, and E, are pushed onto the stack.
・Preimage of HashA0 or HashA1
・Preimage of HashB0 or HashB1
・Preimage of HashE0 or HashE1
If the statement A NAND B == E holds true, this script can be unlocked.
// Reveal Preimage of hashE0 or hashE1
<hashE0/1>
OP_BITCOMMITMENT
OP_TOALTSTACK
// Now the bit value of "E" is on the stack
// Reveal Preimage of hashB0 or hashB1
<hashB0/1>
OP_BITCOMMITMENT
OP_TOALTSTACK
// Now the bit value of "B" is on the stack
// Reveal Preimage of hashA0 or hashA1
<hashA0/1>
OP_BITCOMMITMENT
OP_TOALTSTACK
// Now the bit value of "A" is on the stack
//
// Verify that "A NAND B == E"
//
// Read "B" from alt stack
OP_FROMALTSTACK
#compute A NAND B
OP_NAND
# Read "E" from alt stack
OP_FROMALTSTACK
#Check A NAND B == E
OP_EQUALVERIFY
⚫️Challenge and Response
Challenge and Response is initiated when the Verifier does not agree that the Prover’s assertion is correct. If the assertion’s inconsistencies are identified, the Verifier is entitled to seize the funds of the Prover.
The verifier selects one gate from the circuit, and the prover exposes the input and output (we refer to it as opening a Gate). Both parties repeat this process several times, until either an inconsistency is revealed, or the Verifier exhausted the space of possible challenges.
If the Prover claims that D=1 when one gate is opened, but later claims that D=0 when another gate is opened, the prover has equivocated and the Verifier is able to seize the funds of the Prover.
Note that the Prover is not required to open every Gate.
In the example below, the Verifier asks the Prover to open NAND7, NAND1, NAND3,NAND6 and NAND5 in order.
Initially, when requested to open NAND6, the Prover asserts “I=1”. However, subsequently when asked to open NAND1, NAND3, NAND6, and then NAND5, the Prover is compelled to give the contradictory response of “I=0”. When asked to open NAND6, if the Prover realizes that it will give a contradictory answer regarding the value of I and does not open it, the Verifier is able to seize the funds of the Prover after a certain period of time.
⚫️Challenge Taptree and Response Taptree
A Taptree is used for both parties to commit to the Challenge and Response scheme. A Taptree is a Merkle tree composed of scripts as leaves, and a root (the Taproot) that can be used to tweak a secret key, enabling the use of either a key (the key path) or a script within the Taptree (a script path) to unlock an output.
In the following example, the Verifier selects Gate7 by exposing the unlock condition of the Challenge Taptree and the Prover opens Gate7 by exposing the unlock condition of the Response Taptree.
If the Prover exposes a different value for the same variable (e.g. E=0 && E=1 ), the claim of the Prover is false and the Verifier can get all funds. This model is realized by following Equivocations Taptree.
So far we have learned that the Prover and the Verifier commit to logic gates using a combination of Bitcoin scripts and that Taptrees are used to commit to proof verification based on a Challenge & Response protocol.
In the following sections, we will explain the details of the BitVM protocol.
BitVM Protocol Detail
The following is the flow of a contract using BitVM between the Prover who claims to know the value that satisfies some arbitrary equation and the Verifier.
1. Circuit Construction
The contract is implemented in a programming language and is compiled into a large Binary Circuit; the Prover claims that a certain set of Inputs given to the circuit evaluates to a certain Output.
2.Transaction construction and Pre-signing
A transaction is constructed and pre-signed between Prover and Verifier to commit to the Binary circuit input value proof and verification scheme.
3.Contract execution
Both parties sign and broadcast the Tx1 in figure below to lock their funds. Once the transaction is confirmed, the contract is executed.
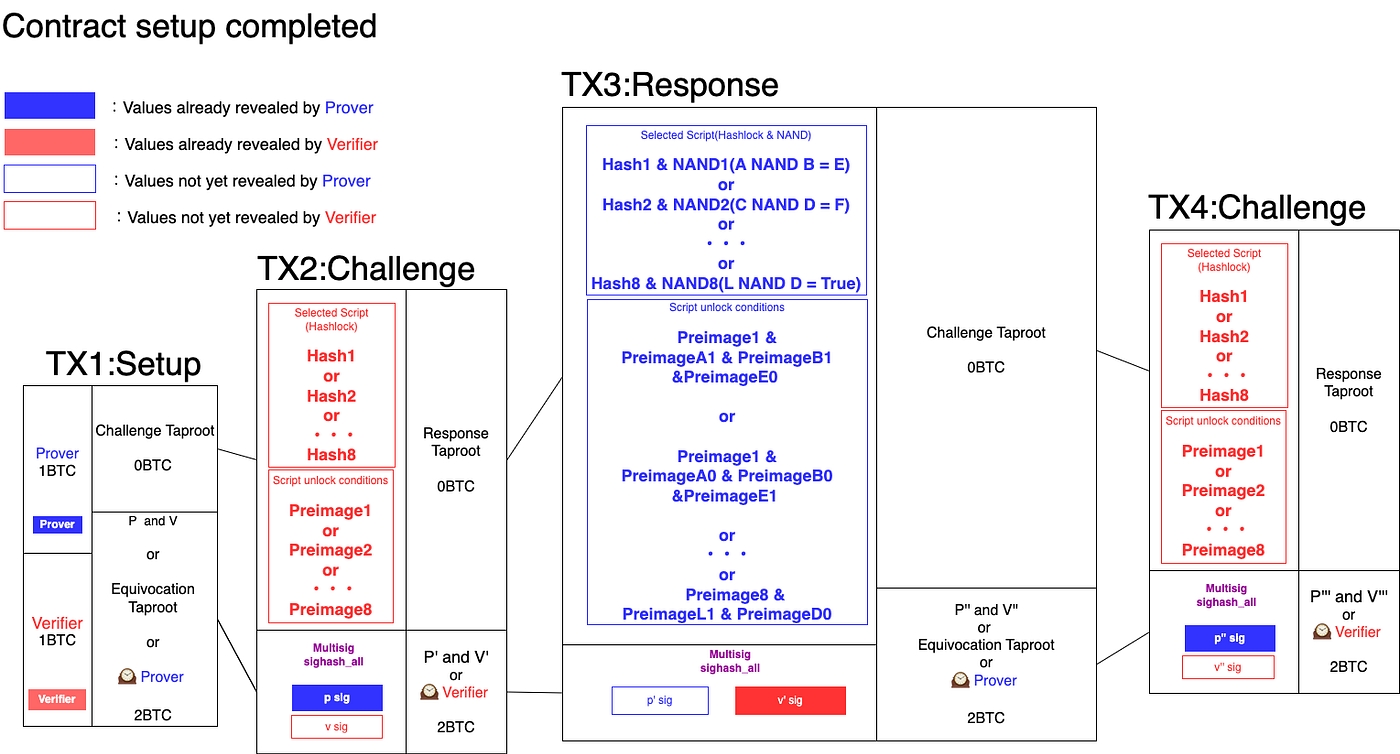
Tx1 is on-chain, while Tx2~Tx4 have not yet been broadcast. Tx2 and Tx4 are held by the Verifier and Tx3 by the Prover.
Please note that the diagram above differs from the original proposal.In the figure above, the output of the first transaction is divided into two parts and sighasg_all is used for pre-signing. If the output is not split, all tapleafs that may be used must be pre-signed. Please see here for the details.
If the Verifier accepts that the Prover’s claim is correct, they skip the ‘4. Challenge & Response’ step and proceed to the ‘5. Settlement’ step. If the Verifier thinks the claim of the Prover is incorrect, they proceed to the ‘4. Challenge & Response’ step.
4.Challenge & Response
The Verifier selects a gate of his choice by exposing the unlock conditions of the Challenge Taptree, and the Prover opens the gate by exposing the unlock conditions of the Response Taptree.
Ideally, this interaction is performed off-chain.(It can also be executed on-chain although)
Both parties repeat this process several times, until either an inconsistency is revealed, or the Verifier exhausted the space of possible challenges.
The following is an example of the Prover and Verifier repeating the Challenge & Response twice off-chain and an inconsistency is revealed.
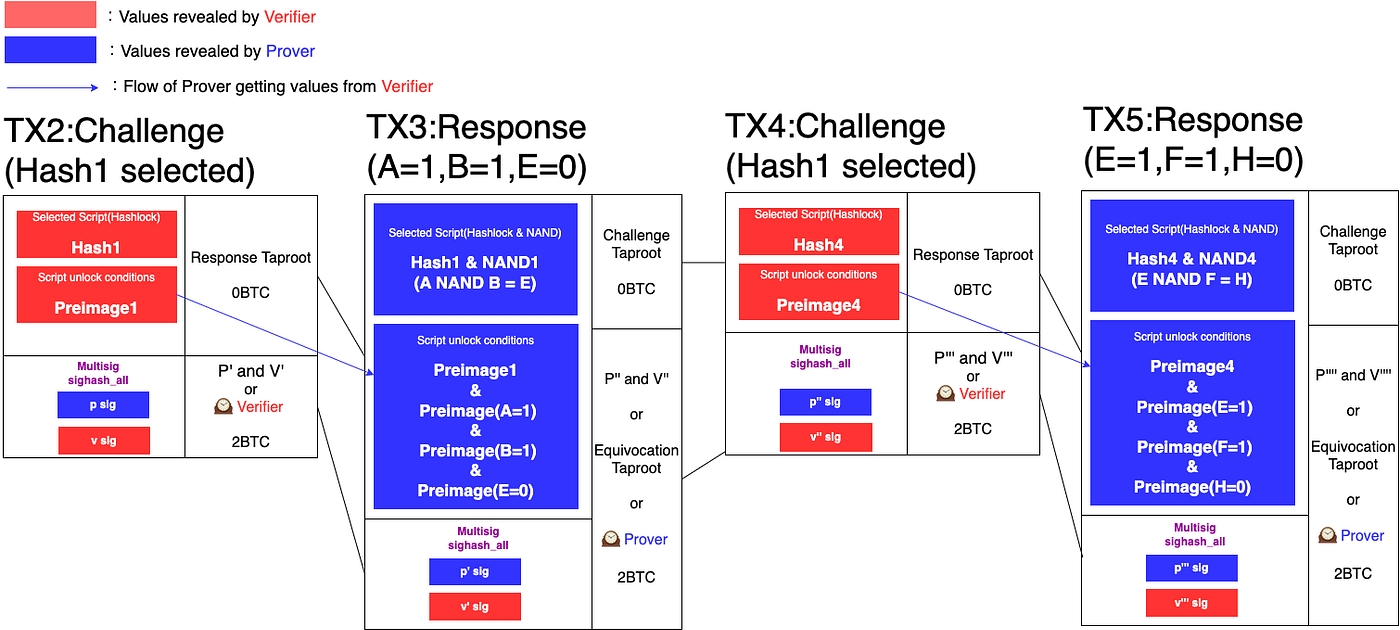
In the first Challenge, the Verifier selects the NAND1 gate, and the Prover exposes its input and output (A=1, B=1, E=0). In the second Challenge, the Verifier selects the NAND4 gate and the Prover exposes its Input, output(E=1,F=1,H=0).
Note that the Prover has an inconsistent response, E=0 the first time and E=1 the second time. Since the Prover has equivocated, the Verifier proceeds to the ‘5. Settlement’ step to seize the Prover’s fund.
5.Settlement
If the Verifier accepts that the Prover’s claim is correct in the ‘3. Contract Execution’ step, they skip the ‘4. Challenge and Response’ step. As long as both parties are cooperative, they can jointly settle any contract with a 2-of-2 signature.
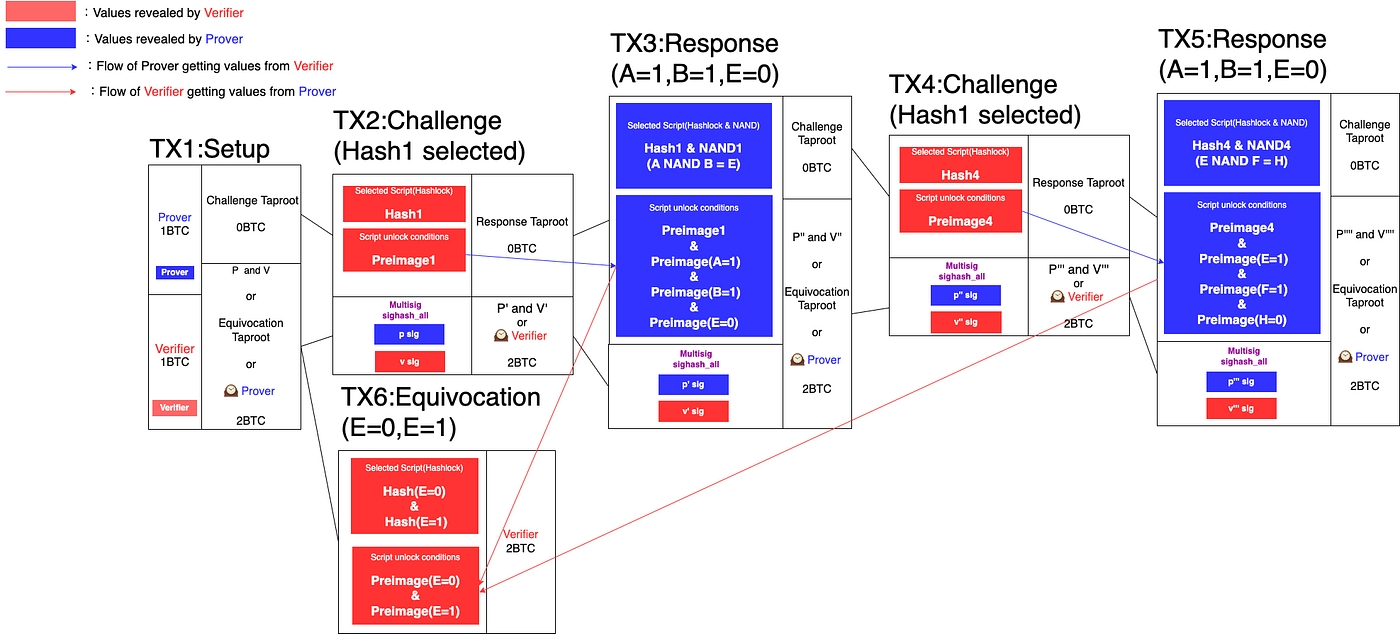
If the Prover has an inconsistent response, in ‘4. Challenge & Response’ step like E=0 the first time and E=1 the second time, The Verifier gets preimage(E=0) and preimage(E=1), which are conditions that Equivocations Taproot address can be unlocked.
The Verifier gets the Prover’s fund by broadcasting Tx6 as below.
Further development
・More high-level opcode for efficiency
Robin Linus states NANDs are used only for the sake of the argument, to abstract away all the complexity of crafting efficient bitcoin scripts.
He believes that in practice using all the available bitcoin script opcodes makes onchain TXs 10x — 100x smaller than when using only NANDs.
That’s why some more high-level opcodes for stuff like u32 addition, u32 xor, u32 rotations are created.
・More general contracts
The proposed model is limited to two parties. More research is needed to develop this model to N:N.
・Scriptless Script BitVM
ZmnSCPxj stated “Scriptless Script BitVM” by replacing hashes and preimages with points and scalars. Using this trick, we can reduce the Tx size and on-chain footprint.
Conclusion
BitVM is a project that enables Turing-complete Bitcoin contracts without soft forks.
If you would like to contribute, here is the Repo.Also you can discuss this topic in Telegram group.
